机械能守恒定律高考题,机械能守恒高考题目

机械能守恒定律中的弹力是指弹簧的弹力(能够使物体形变恢复原状的弹性形变）不包括绳、杆弹力 压力 支持力。

如果是重力和弹力同时对系统做功 那么系统的机械能是守恒的动能EK+重力势能EP1+弹性势能EP‘ =E 动能、重力势能、弹性势能之间发生相互转化。

举例：一劲度系数为k,原长L0竖立在地面上。一质量为m的小球从距弹簧上端高h处自由释放，落到弹簧上，分析从物体落到弹簧上到最低点，动能、重力势能、弹性势能变化情况。

平衡位置Δx=mg/k(速度最大，动能最大）从物体落到弹簧上到最低点，动能先增大后减小、重力势能一直减小、弹性势能一直增大。

一、单个物体的机械能守恒

判断一个物体的机械能是否守恒有两种方法：（1）物体在运动过程中只有重力做功，物体的机械能守恒。 （2）物体在运动过程中不受媒质阻力和摩擦阻力，物体的机械能守恒。

所涉及到的题型有四类：（1）阻力不计的抛体类。（2）固定的光滑斜面类。（3）固定的光滑圆弧类。（4）悬点固定的摆动类。

（1）阻力不计的抛体类

包括竖直上抛；竖直下抛；斜上抛；斜下抛；平抛，只要物体在运动过程中所受的空气阻力不计。那么物体在运动过程中就只受重力作用，也只有重力做功，通过重力做功，实现重力势能与机械能之间的等量转换，因此物体的机械能守恒。

（2）固定的光滑斜面类

在固定光滑斜面上运动的物体，同时受到重力和支持力的作用，由于支持力和物体运动的方向始终垂直，对运动物体不做功，因此，只有重力做功，物体的机械能守恒。

（3）固定的光滑圆弧类

在固定的光滑圆弧上运动的物体，只受到重力和支持力的作用，由于支持力始终沿圆弧的法线方向而和物体运动的速度方向垂直，对运动物体不做功，故只有重力做功，物体的机械能守恒。

（4）悬点固定的摆动类

和固定的光滑圆弧类一样，小球在绕固定的悬点摆动时，受到重力和拉力的作用。由于悬线的拉力自始至终都沿法线方向，和物体运动的速度方向垂直而对运动物体不做功。因此只有重力做功，物体的机械能守恒。

作题方法：

一般选取物体运动的最低点作为重力势能的零势参考点，把物体运动开始时的机械能和物体运动结束时的机械能分别写出来，并使之相等。

注意点：在固定的光滑圆弧类和悬点定的摆动类两种题目中，常和向心力的公式结合使用。这在计算中是要特别注意的。

系统机械能守恒

由两个或两个以上的物体所构成的系统，其机械能是否守恒，要看两个方面

（1）系统以外的力是否对系统对做功，系统以外的力对系统做正功，系统的机械能就增加，做负功，系统的机械能就减少。不做功，系统的机械能就不变。

（2）系统间的相互作用力做功，不能使其它形式的能参与和机械能的转换。 系统内物体的重力所做的功不会改变系统的机械能 系统间的相互作用力分为三类：

1） 刚体产生的弹力：比如轻绳的弹力，斜面的弹力，轻杆产生的弹力等

2） 弹簧产生的弹力：系统中包括有弹簧，弹簧的弹力在整个过程中做功，弹性势能参与机械能的转换。 3） 其它力做功：比如炸药爆炸产生的冲击力，摩擦力对系统对功等。 2

与了机械能的转换，系统的机械能就不再守恒了。

归纳起来，系统的机械能守恒问题有以下四个题型：（1）轻绳连体类（2）轻杆连体类 （3）在水平面上可以自由移动的光滑圆弧类。（4）悬点在水平面上可以自由移动的摆动类。在前两种情况中，轻绳的拉力，斜面的弹力，轻杆产生的弹力做功，使机械能在相互作用的两物体间进行等量的转移，系统的机械能还是守恒的。虽然弹簧的弹力也做功，但包括弹性势能在内的机械能也守恒。但在第三种情况下，由于其它形式的能参

机械能守恒是因为只有保守力做功，在本题里就是因为没有摩擦，拉力的功只是起到能量在两物体间转移作用。

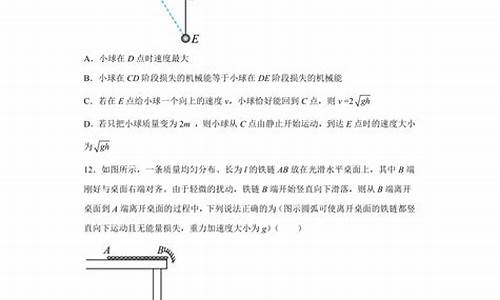
可以这么想，截止到B落地之前，绳子对B做了功，而且拉力竖直向上所以是负功，由于这是一根绳子，力处处相等，所以拉力也会对A做功，而且是正的。又因为在B落地之前，绳子是紧绷的，所以B走了多少，绳子就会带动A走相同的距离，所以绳子对两物体做的正负功数值上相等，代数和为零。

但是A、B之间的绳长应该是2H，B落地后速度变为零，绳子属于舒张状态，不对继续上滑的A施力，A仍有速度，且已走到了距地面3/4H处，在上升H/4就到达顶端。之后A继续上滑，只受重力，并且恰好到达顶端。

综合上述分析，可列式如下（动能定理），

1/2*(m1+m2)v^2=m2g*h/2-m1g*h/4

1/2m1*v^2-m1*g*h/4=0

用第二个方程可以表示出速度v，然后把球出的速度带回第一个方程，可以解出

m1=1/2*m2

不知对不对，希望能对你有帮助。