高中数学函数高考题_高中函数高考题目

1.高一数学必修一函数问题

2.一个数学高中的三角函数题，求解

3.高中数学函数例题以及解析？

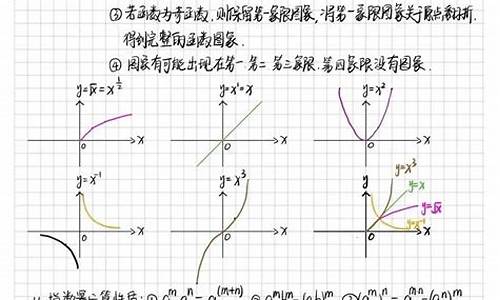
因为函数f(x+4)为偶函数

可设f(x+4)=-x^2

则f(x)=-（x-4）^2，为函数f(x+4)向右平移4个单位

符合条件函数f(x)在区间(4,+00)上为减函数

而f(x)=-（x-4）^2的对称轴为x=4

所以函数f(x)的图像关于x=4对称。

高一数学必修一函数问题

第一步：求b

已知f(x)，所以可求f'(x)，即f'(x)=X^2-(a+1)X+b

又由题意可知（0,0）满足f'(x)=X^2-(a+1)X+b ，所以将点（0，0）代入f'(x)=X^2-(a+1)X+b可求 得：b=0

1）因为a=1，b=0 所以f'(x)=X^2-(a+1)X+b=X^2-2X

当X=3时， K=f'(3)=3（用K表示函数f(x)在X=3处的斜率）

因为f(x)=(1/3)x^3-x^2+1 ，所以f(3)=1

所以可 设函数f(x)的图像在X=3处的切线方程为y=3x+B，（关键就是求B了）

由题意可知点（3，1）在直线y=3x+B上，所以代入点，可求得B= -8

所以函数f(x)的图像在X=3处的切线方程为y=3x-8

2）由题意可知X^2-(a+1)X=-9 ，即 存在方程X^2-(a+1)X +9=0

问题2就变成了：如果方程X^2-(a+1)X +9=0在X<0处有解，求a的最大值

这个就应该是高二的知识了，你个应该自己思考啊！

一个数学高中的三角函数题，求解

括号里的内容为解释，解答过程中无需写

①

（1）证明：

设x1,x2∈R，x1＜x2

f(x+y)=f(x)+f(y)-1，即f(x+y)-f(x)=f(y)-1

f(x2)-f(x1)=f(x2-x1)-1

∵x1＜x2

∴x2-x1＞0

由条件可得，f(x2-x1)＞1

∴f(x2-x1)-1＞0

即f(x2)-f(x1)＞0

∴该函数为增函数

（2）

∵该函数为增函数（已证）

∴当x=1时，f(x)取得最小值；当x=2时，f(x)取得最大值

将3拆分成1+2，将2再拆分成1+1

f(3)=f(2)+f(1)-1=f(1)+f(1)-1+f(1)-1=3f(1)-2=4

解得f(1)=2

f(2)=2f(1)-1=3

∴f(x)在[1,2]上的最大值为3，最小值为2。

②

∵该函数为奇函数，f(1)=(a+1)/b+c=2

∴f(-1)=(a+1)/-b+c=-2

分子相同，结果互为相反数，则分母互为相反数

解得c=0

f(1)=(a+1)/b=2 即a+1=2b

f(2)=(4a+1)/2b＜3

即(4a+1)/(a+1)＜3

移项，通分，可化为(4a+1-3a-3)/(a+1)＜0即(a-2)/(a+1)＜0，分数值小于0，则分子分母异号，观察式子，分子小于分母，因而分子＜0，分母＞0

解得-1＜a＜2

∵a∈Z，∴a=1或0

当a=0时，代入(a+1)/b=2得，b=1/2，与b∈Z矛盾，故舍去。

当a=1时，代入(a+1)/b=2得，b=1，符合。

综上所述，a=1,b=1,c=0

③

原函数是个固定位置的图像开口向上有最小值的二次函数，因而需要分三种情况讨论，图像的对称轴在区间[t,t+2]的左边，之间，右边，因而g(t)是个分段函数。图像电脑上实在不好画，你自己画一个

f(x)=x?-4x-1=(x-2)?-5

图像的对称轴为直线x=2

当t＞2时，这段函数为增函数，当x=t时，函数取得最小值(t-2)?-5

当t＜2＜t+2时，函数最小值为-5

当t+2＜2即t＜0时，这段函数为减函数，当x=t+2时，函数取得最小值t?-5

综上所述，

g(t)={ (t-2)?-5 t＞2

-5 t＜2＜t+2

t?-5 t＜0

分段函数你会写的吧，那个很大的左大括号和空格实在弄不出来啊

由分段函数解析式可得，该分段函数的最小值为-5

④

结论： F(x)=1\f(x)在(-∞,0)上是减函数

证明：

设x1,x2∈(-∞,0),x1<x2

则 -x1>-x2>0

∵f(x)在(0,+∞)上是增函数，且f(x)＜0

∴ 0>f(-x1)>f(-x2)

又f(x)是奇函数

∴ 0>-f(x1)>-f(x2)

0<f(x1)<f(x2)

∴1/f(x1)>1/f(x2)

即F(x1)>F(x2)

∴F(x)=1\f(x)在(-∞,0)上是减函数

这个增减+奇偶什么的题目，理解不了的地方就画图

⑤

设x1,x2∈[1,3]，x1＜x2

f(x2)-f(x1)=(x2-1)/(x2+1)-(x1-1)/(x1+1)=2(x2-x1)/(x1x2+x1+x2+1)通分你可以的

∵x1＜x2

∴2(x2-x1)＞0

又x1,x2∈[1,3]

∴x1x2+x1+x2+1＞0

即f(x2)-f(x1)＞0

∴该函数为增函数

∴当x=1时，函数取得最小值f(1)=0

当x=3时，函数取得最大值f(3)=1/2

综上所述，该函数的最大值为1/2，最小值为0

高中数学函数例题以及解析？

等式左边=√2(sinx-cosx)

=2sin(x-π/4)

等式右边=3(siny)^2-6siny+5

=3(siny-1)^2+2

等式左边最大值为2，右边最小值为2，所以两边均等于2时，等式才成立，所以：

sin(x-π/4)=1

siny=1

由于x、y∈(0，2π)

x=3π/4

y=π/2

所以：x+y=5π/4

一、基本概念：

1、 数列的定义及表示方法：

2、 数列的项与项数：

3、 有穷数列与无穷数列：

4、 递增（减）、摆动、循环数列：

5、 数列{an}的通项公式an：

6、 数列的前n项和公式Sn:

7、 等差数列、公差d、等差数列的结构：

8、 等比数列、公比q、等比数列的结构：

二、基本公式：

9、一般数列的通项an与前n项和Sn的关系：an=

10、等差数列的通项公式：an=a1+(n-1)d an=ak+(n-k)d (其中a1为首项、ak为已知的第k项) 当d≠0时，an是关于n的一次式；当d=0时，an是一个常数。

11、等差数列的前n项和公式：Sn= Sn= Sn=

当d≠0时，Sn是关于n的二次式且常数项为0；当d=0时（a1≠0），Sn=na1是关于n的正比例式。

12、等比数列的通项公式： an= a1 qn-1 an= ak qn-k

(其中a1为首项、ak为已知的第k项，an≠0)

13、等比数列的前n项和公式：当q=1时，Sn=n a1 (是关于n的正比例式)；

当q≠1时，Sn= Sn=

三、有关等差、等比数列的结论

14、等差数列{an}的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m - S3m、……仍为等差数列。

15、等差数列{an}中，若m+n=p+q，则

16、等比数列{an}中，若m+n=p+q，则

17、等比数列{an}的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m - S3m、……仍为等比数列。

18、两个等差数列{an}与{bn}的和差的数列{an+bn}、{an-bn}仍为等差数列。

19、两个等比数列{an}与{bn}的积、商、倒数组成的数列

{an bn}、 、 仍为等比数列。

20、等差数列{an}的任意等距离的项构成的数列仍为等差数列。

21、等比数列{an}的任意等距离的项构成的数列仍为等比数列。

22、三个数成等差的设法：a-d,a,a+d；四个数成等差的设法：a-3d,a-d,,a+d,a+3d

23、三个数成等比的设法：a/q,a,aq；

四个数成等比的错误设法：a/q3,a/q,aq,aq3 (为什么？)

24、{an}为等差数列，则 (c>0)是等比数列。

25、{bn}（bn>0）是等比数列，则{logcbn} (c>0且c 1) 是等差数列。

26. 在等差数列 中：

（1）若项数为 ，则

（2）若数为 则， ，

27. 在等比数列 中：

（1） 若项数为 ，则

（2）若数为 则，

四、数列求和的常用方法：公式法、裂项相消法、错位相减法、倒序相加法等。关键是找数列的通项结构。

28、分组法求数列的和：如an=2n+3n

29、错位相减法求和：如an=(2n-1)2n

30、裂项法求和：如an=1/n(n+1)

31、倒序相加法求和：如an=

32、求数列{an}的最大、最小项的方法：

① an+1-an=…… 如an= -2n2+29n-3

② (an>0) 如an=

③ an=f(n) 研究函数f(n)的增减性 如an=

33、在等差数列 中,有关Sn 的最值问题——常用邻项变号法求解：

(1)当 >0,d<0时，满足 的项数m使得 取最大值.

(2)当 <0,d>0时，满足 的项数m使得 取最小值。

在解含绝对值的数列最值问题时,注意转化思想的应用。

六、平面向量

1．基本概念：

向量的定义、向量的模、零向量、单位向量、相反向量、共线向量、相等向量。

2． 加法与减法的代数运算：

(1) ．

(2)若a=（ ）,b=（ ）则a b=（ ）．

向量加法与减法的几何表示：平行四边形法则、三角形法则。

以向量 = 、 = 为邻边作平行四边形ABCD，则两条对角线的向量 = + , = － , = －

且有｜ ｜－｜ ｜≤｜ ｜≤｜ ｜+｜ ｜．

向量加法有如下规律： ＋ = ＋ (交换律); +( +c)=( + )+c （结合律）;

+0= ＋(－ )=0.

3．实数与向量的积：实数 与向量 的积是一个向量。

(1)｜ ｜=｜ ｜·｜ ｜;

(2) 当 ＞0时， 与 的方向相同；当 ＜0时， 与 的方向相反；当 =0时， =0．

(3)若 =（ ），则 · =（ ）．

两个向量共线的充要条件：

(1) 向量b与非零向量 共线的充要条件是有且仅有一个实数 ，使得b= ．

(2) 若 =（ ）,b=（ ）则 ‖b ．

平面向量基本定理：

若e1、e2是同一平面内的两个不共线向量，那么对于这一平面内的任一向量 ，有且只有一对实数 ， ，使得 = e1+ e2．

4．P分有向线段 所成的比：

设P1、P2是直线 上两个点，点P是 上不同于P1、P2的任意一点，则存在一个实数 使 = ， 叫做点P分有向线段 所成的比。

当点P在线段 上时， ＞0；当点P在线段 或 的延长线上时， ＜0；

分点坐标公式：若 = ； 的坐标分别为（ ）,（ ）,（ ）；则 （ ≠－1）， 中点坐标公式： ．

5． 向量的数量积：

（1）．向量的夹角：

已知两个非零向量 与b，作 = , =b,则∠AOB= （ ）叫做向量 与b的夹角。

（2）．两个向量的数量积：

已知两个非零向量 与b，它们的夹角为 ，则 ·b=｜ ｜·｜b｜cos ．

其中｜b｜cos 称为向量b在 方向上的投影．

（3）．向量的数量积的性质：

若 =（ ）,b=（ ）则e· = ·e=｜ ｜cos (e为单位向量);

⊥b ·b=0 （ ，b为非零向量）;｜ ｜= ;

cos = = ．

(4) ．向量的数量积的运算律：

·b=b· ;( )·b= ( ·b)= ·( b);( ＋b)·c= ·c+b·c．

6.主要思想与方法：

本章主要树立数形转化和结合的观点，以数代形，以形观数，用代数的运算处理几何问题，特别是处理向量的相关位置关系，正确运用共线向量和平面向量的基本定理，计算向量的模、两点的距离、向量的夹角，判断两向量是否垂直等。由于向量是一新的工具，它往往会与三角函数、数列、不等式、解几等结合起来进行综合考查，是知识的交汇点。

七、立体几何

1.平面的基本性质：掌握三个公理及推论，会说明共点、共线、共面问题。

能够用斜二测法作图。

2.空间两条直线的位置关系：平行、相交、异面的概念；

会求异面直线所成的角和异面直线间的距离；证明两条直线是异面直线一般用反证法。

3.直线与平面

①位置关系：平行、直线在平面内、直线与平面相交。

②直线与平面平行的判断方法及性质,判定定理是证明平行问题的依据。

③直线与平面垂直的证明方法有哪些？

④直线与平面所成的角：关键是找它在平面内的射影，范围是{00.900}

⑤三垂线定理及其逆定理：每年高考试题都要考查这个定理. 三垂线定理及其逆定理主要用于证明垂直关系与空间图形的度量.如：证明异面直线垂直，确定二面角的平面角，确定点到直线的垂线.

4.平面与平面

(1)位置关系：平行、相交，（垂直是相交的一种特殊情况）

(2)掌握平面与平面平行的证明方法和性质。

(3)掌握平面与平面垂直的证明方法和性质定理。尤其是已知两平面垂直，一般是依据性质定理，可以证明线面垂直。

(4)两平面间的距离问题→点到面的距离问题→

(5)二面角。二面角的平面交的作法及求法：

①定义法，一般要利用图形的对称性；一般在计算时要解斜三角形；

②垂线、斜线、射影法，一般要求平面的垂线好找，一般在计算时要解一个直角三角形。

③射影面积法，一般是二面交的两个面只有一个公共点，两个面的交线不容易找到时用此法?

回